una serie de Taylor es una aproximación de funciones mediante una serie de potencias o suma de potencias enteras de polinomios como  llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto
llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto  suficientemente derivable sobre la función y un entorno sobre el cual
converja la serie. Si esta serie está centrada sobre el punto cero,
suficientemente derivable sobre la función y un entorno sobre el cual
converja la serie. Si esta serie está centrada sobre el punto cero, 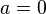 , se le denomina serie de McLaurin.
, se le denomina serie de McLaurin.
Esta aproximación tiene tres ventajas importantes: llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto
llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto  suficientemente derivable sobre la función y un entorno sobre el cual
converja la serie. Si esta serie está centrada sobre el punto cero,
suficientemente derivable sobre la función y un entorno sobre el cual
converja la serie. Si esta serie está centrada sobre el punto cero, 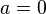 , se le denomina serie de McLaurin.
, se le denomina serie de McLaurin.
- la derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales;
- se puede utilizar para calcular valores aproximados de funciones;
- es posible calcular la optimidad de la aproximación.

A medida que aumenta el grado del polinomio de MacLaurin, se aproxima a la función. Se ilustran las aproximaciones de MacLaurin a sen(x), centradas en 0, de grados 1, 3, 5, 7, 9, 11 y 13

La gráfica de la función exponencial (en azul), y la suma de los primeros n+1 términos de su serie de Taylor en torno a cero (en rojo).
La serie de Taylor de una función f real o compleja ƒ(x) infinitamente diferenciable en el entorno de un número real o complejo a es la siguiente serie de potencias:
que puede ser escrito de una manera más compacta como la siguiente suma:
,
donde:
- n! es el factorial de n
- f (n)(a) denota la n-ésima derivada de f para el valor a de la variable respecto de la cual se deriva.
 son ambos definidos como 1 (
son ambos definidos como 1 ( = 1). En caso de ser a = 0, como ya se mencionó, la serie se denomina también de MacLaurin.
= 1). En caso de ser a = 0, como ya se mencionó, la serie se denomina también de MacLaurin.Cabe destacar que en una serie de Taylor de potencias centrada en a de la forma
 siempre se puede hacer el cambio de variable
siempre se puede hacer el cambio de variable 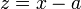 (con lo que
(con lo que 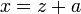 en la función a desarrollar original) para expresarla como
en la función a desarrollar original) para expresarla como 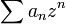 centrada en 0. Luego hay que deshacer el cambio de variable. Por ejemplo, si se quiere desarrollar la función
centrada en 0. Luego hay que deshacer el cambio de variable. Por ejemplo, si se quiere desarrollar la función 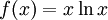 alrededor de a = 1 se puede tomar
alrededor de a = 1 se puede tomar  , de manera que se desarrollaría
, de manera que se desarrollaría  centrada en 0.
centrada en 0.Función exponencial y logaritmo natural
Serie geométrica
Funciones trigonométricas
-
- Donde Bs son los Números de Bernoulli.
Funciones hiperbólicas
Función W de Lambert
La serie de Taylor se puede generalizar a funciones de
 variables:
variables: es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:
es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:Un polinomio de Taylor de segundo grado puede ser escrito de manera compacta así:
 es el gradiente y
es el gradiente y 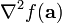 es la matriz hessiana. Otra forma:
es la matriz hessiana. Otra forma:
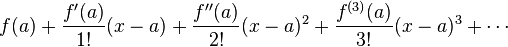




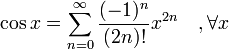









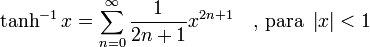


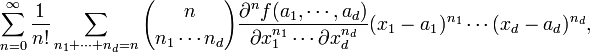
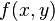

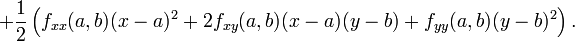
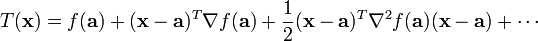




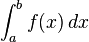 representa el área de la región delimitada por la gráfica de f y el eje x, desde x=a hasta x=b. Primero se divide el intervalo [a,b] en n subintervalos, cada uno de ancho
representa el área de la región delimitada por la gráfica de f y el eje x, desde x=a hasta x=b. Primero se divide el intervalo [a,b] en n subintervalos, cada uno de ancho  .
.![\int_a^b f(x)\, dx \sim \frac{h}{2} [f(a)+2f(a+h)+2f(a+2h)+...+f(b)]](http://upload.wikimedia.org/math/8/5/b/85ba9814a3fc9015d6bceddda5883827.png)
 y n es el número de divisiones
y n es el número de divisiones![\int_a^b f(x) dx \sim \frac{b-a}{n} \left[ \frac{f(a) + f(b)}{2} + \sum_{k=1}^{n-1} f\left(a + k \frac{b-a}{n}\right) \right]](http://upload.wikimedia.org/math/b/7/8/b78df5203c74d8f9bb2947cbf58caac3.png)


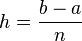
 .
.![\frac{h}{2} [f(a)+2f(a+h)+2f(a+2h)+...+f(b)]](http://upload.wikimedia.org/math/3/b/9/3b96e7e506a0c4e4b9faeda6fecc72ed.png)
![\frac{1}{2} \cdot \frac{1}{6} [3(1)+2[3(1+1\cdot \frac{1}{6})]+2[3(1+2\cdot \frac{1}{6})]+2[3(1+3\cdot \frac{1}{6})]+2[3(1+4\cdot \frac{1}{6})]+2[3(1+5\cdot \frac{1}{6})]+3(2)] = 4.5](http://upload.wikimedia.org/math/0/3/9/0390f869f9ff3628627f890664a961ad.png)