es un método de integración numérica, es
decir, un método para calcular aproximadamente el valor de la integral definida

La regla se basa en aproximar el valor de la integral de f(x)
por el de la función lineal que pasa a
través de los puntos (a, f(a)) y (b, f(b)).
La integral de ésta es igual al área del trapecio bajo la gráfica
de la función lineal. Se sigue que

y donde el término error corresponde a:

Siendo  un número perteneciente
al intervalo [a,b].
un número perteneciente
al intervalo [a,b].
 un número perteneciente
al intervalo [a,b].
un número perteneciente
al intervalo [a,b].
La función f(x) (en azul) es aproximada por la función lineal (en rojo).
La regla del trapecio compuesta o regla de los trapecios es una forma de aproximar una integral definida utilizando n trapecios. En la formulación de este método se supone que f es continua y positiva en el intervalo [a,b]. De tal modo la integral definida
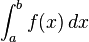 representa el área de la región delimitada por la gráfica de f y el eje x, desde x=a hasta x=b. Primero se divide el intervalo [a,b] en n subintervalos, cada uno de ancho
representa el área de la región delimitada por la gráfica de f y el eje x, desde x=a hasta x=b. Primero se divide el intervalo [a,b] en n subintervalos, cada uno de ancho  .
.Después de realizar todo el proceso matemático se llega a la siguiente fórmula:
 y n es el número de divisiones
y n es el número de divisionesLa expresión anterior también se puede escribir como:
Ejemplo
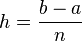
 .
.Y ahora se sustituye en la fórmula
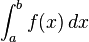 =
= ![\frac{h}{2} [f(a)+2f(a+h)+2f(a+2h)+...+f(b)]](http://upload.wikimedia.org/math/3/b/9/3b96e7e506a0c4e4b9faeda6fecc72ed.png)
En este caso no se comete ningún error en el cálculo (el resultado es exacto) porque la función sujeta a integración es lineal.
![\int_a^b f(x)\, dx \sim \frac{h}{2} [f(a)+2f(a+h)+2f(a+2h)+...+f(b)]](http://upload.wikimedia.org/math/8/5/b/85ba9814a3fc9015d6bceddda5883827.png)
![\int_a^b f(x) dx \sim \frac{b-a}{n} \left[ \frac{f(a) + f(b)}{2} + \sum_{k=1}^{n-1} f\left(a + k \frac{b-a}{n}\right) \right]](http://upload.wikimedia.org/math/b/7/8/b78df5203c74d8f9bb2947cbf58caac3.png)


![\frac{1}{2} \cdot \frac{1}{6} [3(1)+2[3(1+1\cdot \frac{1}{6})]+2[3(1+2\cdot \frac{1}{6})]+2[3(1+3\cdot \frac{1}{6})]+2[3(1+4\cdot \frac{1}{6})]+2[3(1+5\cdot \frac{1}{6})]+3(2)] = 4.5](http://upload.wikimedia.org/math/0/3/9/0390f869f9ff3628627f890664a961ad.png)