2.- Tipo de Errores
24 abr 2015
Comparación de gráficas utilizando distintos tipos de software
Graph
Esta aplicación es sencilla de usar se puede dibujar gráficas de funciones matemáticas en un sistema de coordenadas, de forma sencilla y precisa. Se puede trabajar tanto con gráficas normales como con funciones de parámetro.
Soporta una amplia variedad de funciones ya integradas (seno, coseno, tangente, logaritmo, raíz cuadrada, factorial...) y se pueden dibujar en diferentes colores y estilos de línea para distinguirlas fácilmente unas de otras, así como añadir sombras y puntos a todo el sistema de coordinada
Ejemplo 1: x^3-4x^2+3x-2
Esta aplicación es sencilla de usar se puede dibujar gráficas de funciones matemáticas en un sistema de coordenadas, de forma sencilla y precisa. Se puede trabajar tanto con gráficas normales como con funciones de parámetro.
Soporta una amplia variedad de funciones ya integradas (seno, coseno, tangente, logaritmo, raíz cuadrada, factorial...) y se pueden dibujar en diferentes colores y estilos de línea para distinguirlas fácilmente unas de otras, así como añadir sombras y puntos a todo el sistema de coordinada
Ejemplo 1: x^3-4x^2+3x-2
Ejemplo 2: 2x^3+5x^2-3
Ejemplo 3: 2x^4+3x-2
Ejemplo 4: 2x^3-3
Tipo de Errores
Los errores numéricos se generan con el uso de aproximaciones para representar las operaciones y cantidades matemáticas.
Estos incluyen de truncamiento que resultan de representar aproximadamente un procedimiento matemático exacto, y los errores de redondeo, que resultan de presentar aproximadamente números exactos. Para los tipos de errores, la relación entre el resultado exacto o verdadero y el aproximado se resuelve implementando la siguiente formula:
E = P* - P
Pueden ser calculas mediante una forma directa o indirecta, la indirecta consiste en calcular con la que da el aparato y la directa empleando la formula
Existen distintos tipos de errores por ejemplo:
Error Absoluto
Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
Sin embargo, para facilitar el manejo y el análisis se emplea el error absoluto definido como:
El error relativo también se puede multiplicar por el 100% para expresarlo como:
EA = | P* - P |
Error Relativo
Es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. no tiene unidades.
Y el error relativo como:
ER = | P* - P| / P , si P =/ 0
ERP = ER x 100
Ejemplo:
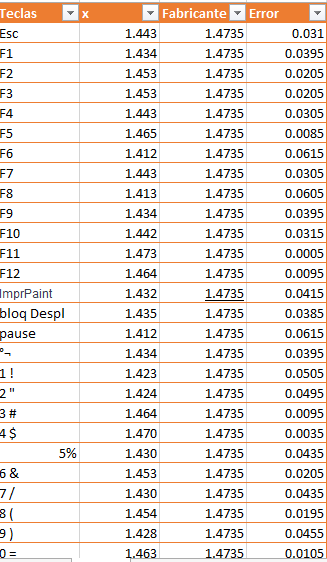
Medir cada uno de los botones de un teclado para posteriormente compararlas con las medidas que no ofrece el fabricante y encontrar el error en cada medida de los botones.
En este caso se utilizo un teclado Hp
En las tablas se representan las medidas de los botones del teclado donde X representa las medidas que fueron tomadas por nosotros, y la columna Fabricante son las medidas que nos ofrece el fabricante comparando ambas columnas obtenemos el error de cada botón
Grafica representando los errores de los botones
Método de Bisección
Método de Bisección
El método de bisección es un algoritmo de búsqueda de raíces que trabaja en dividir el intervalo en 2 subintervalos de igual magnitud, reteniendo el subintervalo en donde f cambia de signo, para conservar al menos una raíz o cero, y repetir el proceso varias veces.
Si f es una función continua sobre el intervalo [a,b] y si f(a) f(b)<0, entonces f debe tener un cero en (a,b). Dado que f(a)f(b)<0, la función cambia de signo en el intervalo [a,b] y por lo tanto tiene por lo menos un cero en el intervalo.
Paso 1
Se deben elegir los valores iniciales Xa y Xb, de tal forma de que la función cambie de signo:
f(Xa)f(Xb) < 0
La primera aproximación de la raíz se determina con la siguiente formula:
Paso 3
Paso 4
Si f(Xa)f(Xb) = 0 ó Error = | Xpm – Xpm – 1 | < Tolerancia
Xpm es el punto medio de la interacción actual y Xpm-1 es el punto medio de la interacción anterior
Paso 5
Para calcular el error relativo porcentual se emplea la siguiente formula:
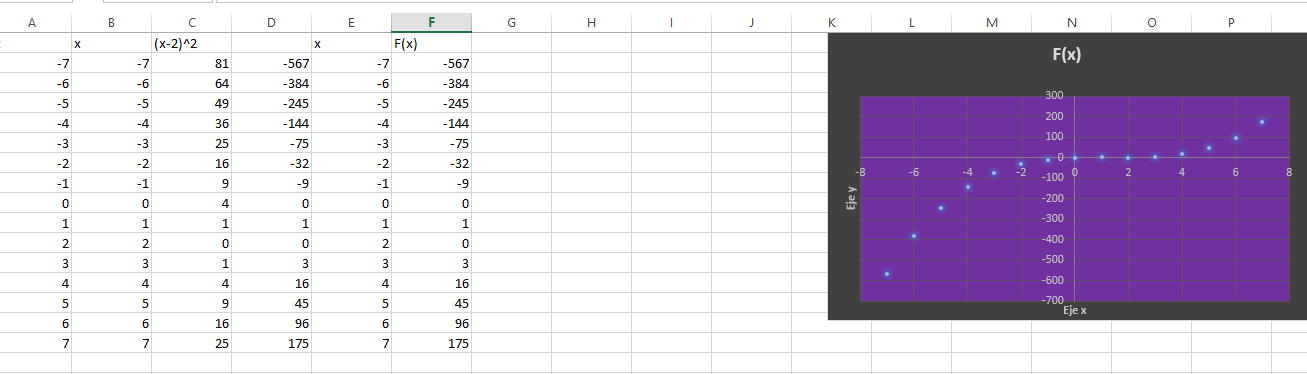
Ejemplo 1: (x-2)^2
Ejemplo 2: x^3+4x^2+3x-2
Ejemplo 3: 2x^3+5x
Ejemplo 4: 2x^4+3x-2
Suscribirse a:
Comentarios (Atom)