Método de Bisección
El método de bisección es un algoritmo de búsqueda de raíces que trabaja en dividir el intervalo en 2 subintervalos de igual magnitud, reteniendo el subintervalo en donde f cambia de signo, para conservar al menos una raíz o cero, y repetir el proceso varias veces.
Si f es una función continua sobre el intervalo [a,b] y si f(a) f(b)<0, entonces f debe tener un cero en (a,b). Dado que f(a)f(b)<0, la función cambia de signo en el intervalo [a,b] y por lo tanto tiene por lo menos un cero en el intervalo.
Paso 1
Se deben elegir los valores iniciales Xa y Xb, de tal forma de que la función cambie de signo:
f(Xa)f(Xb) < 0
La primera aproximación de la raíz se determina con la siguiente formula:
Paso 3
Paso 4
Si f(Xa)f(Xb) = 0 ó Error = | Xpm – Xpm – 1 | < Tolerancia
Xpm es el punto medio de la interacción actual y Xpm-1 es el punto medio de la interacción anterior
Paso 5
Para calcular el error relativo porcentual se emplea la siguiente formula:
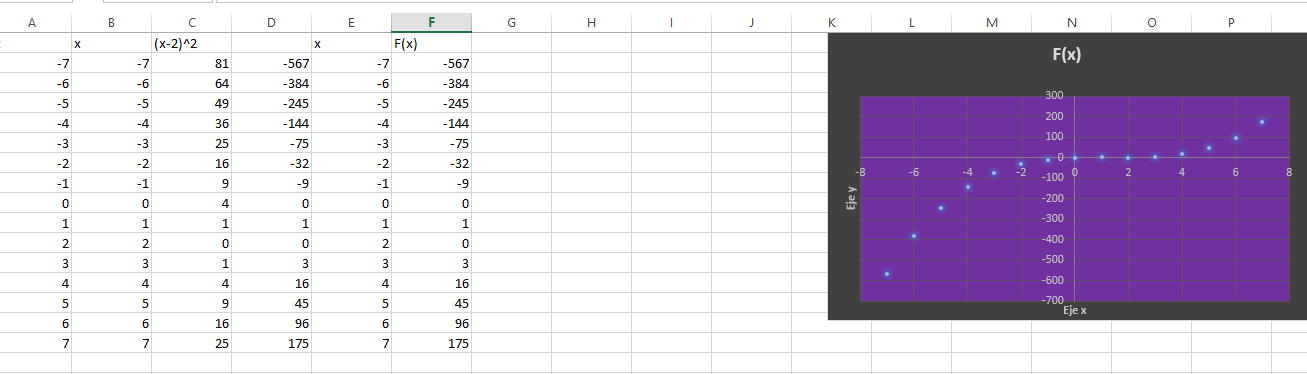
Ejemplo 1: (x-2)^2
Ejemplo 2: x^3+4x^2+3x-2
Ejemplo 3: 2x^3+5x
Ejemplo 4: 2x^4+3x-2