Estos incluyen de truncamiento que resultan de representar aproximadamente un procedimiento matemático exacto, y los errores de redondeo, que resultan de presentar aproximadamente números exactos. Para los tipos de errores, la relación entre el resultado exacto o verdadero y el aproximado se resuelve implementando la siguiente formula:
E = P* - P
Pueden ser calculas mediante una forma directa o indirecta, la indirecta consiste en calcular con la que da el aparato y la directa empleando la formula
Existen distintos tipos de errores por ejemplo:
Error Absoluto
Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
Sin embargo, para facilitar el manejo y el análisis se emplea el error absoluto definido como:
El error relativo también se puede multiplicar por el 100% para expresarlo como:
EA = | P* - P |
Error Relativo
Es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. no tiene unidades.
Y el error relativo como:
ER = | P* - P| / P , si P =/ 0
ERP = ER x 100
Ejemplo:
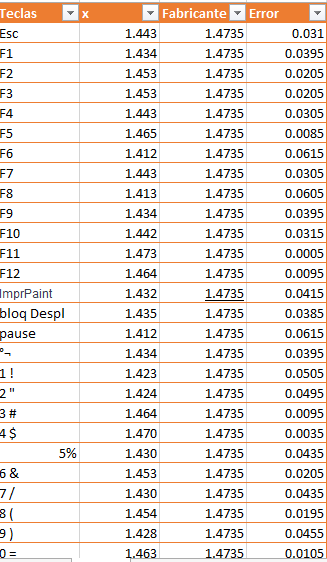
Medir cada uno de los botones de un teclado para posteriormente compararlas con las medidas que no ofrece el fabricante y encontrar el error en cada medida de los botones.
En este caso se utilizo un teclado Hp
En las tablas se representan las medidas de los botones del teclado donde X representa las medidas que fueron tomadas por nosotros, y la columna Fabricante son las medidas que nos ofrece el fabricante comparando ambas columnas obtenemos el error de cada botón
Grafica representando los errores de los botones